2024年辽宁大学非全日制研究生招生考试《数学分析》考试大纲
1.实数集与函数
1.1 掌握实数概念及其基本性质。掌握实数绝对值的概念和有关的不等式。
1.2 掌握邻域概念, 掌握确界定理。
1.3 掌握函数的概念及各种表示方法,掌握复合函数和反函数的概念。
1.4 掌握有界函数与无界函数、单调函数、奇函数和偶函数、周期函数等概念。
1.5 掌握六类基本初等函数的定义和性质。
1.6 掌握常用的几个非初等函数，如符号函数，狄利克雷函数等。
2. 数列极限
2.1 掌握数列极限的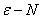
的定义, 会使用“
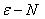语言”证明数列的极限。
2.2 正确理解和掌握收敛数列的性质。
2.3 掌握单调有界原理,致密性定理及Cauchy收敛准则。
3. 函数极限
3.1 掌握函数极限的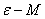
和
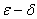定义。
3.2 掌握函数极限的性质。
3.3 掌握函数极限存在的条件, 掌握归结原则及柯西准则。
3.4 掌握重要极限
和
及其应用。
3.5 正确理解和掌握无穷大和无穷小的概念及无穷小的阶。
4. 函数的连续性
4.1 掌握连续函数的概念, 掌握间断点及其分类。
4.2 掌握连续函数的局部性质,掌握闭区间上连续函数的性质。
4.3 掌握反函数的连续性,掌握函数的一致连续性。
4.4 掌握初等函数在其定义域上的连续性。
5. 导数与微分
5.1 掌握导数的概念及其几何意义。
5.2 掌握求导法则,掌握参变量函数的导数法则, 掌握高阶导数的求法。
5.3 掌握微分的概念及其几何意义。
5.4 掌握微分的运算法则,了解高阶微分,了解微分在近似计算中的应用。
6. 微分中值定理及其应用
6.1 熟练掌握中值定理的条件、结论和证明方法。
6.2 掌握不定式极限的求法,熟练掌握洛必达法则及其应用。
6.3 掌握泰勒公式，掌握用多项式逼近函数的思想。
6.4 会分析函数的性态,会求函数的单调区间和极值，会判断函数的凸性和拐点,会较完善地作出函数的图形。
由于篇幅有限，无法为同学全面展示，想要了解更多，请点击下面附件进行下载。
您填的信息已提交,老师会在24小时之内与您联系
如果还有其他疑问请拨打以下电话
热门简章
更多-
地点： 辽宁6.00万
辽宁大学法律 3年学制 周末班} -
地点： 辽宁6.00万
辽宁大学会计 3年学制 周末班}
-
地点： 辽宁6.00万
辽宁大学法律 3年学制 周末班}
-
地点： 辽宁5.00万
辽宁大学旅游管理 2.5年学制 周末班}
-
地点： 辽宁5.80万
辽宁大学公共管理(MPA) 2.5年学制 周末班}
-
地点： 辽宁5.00万
辽宁大学广播电视 3年学制 周末班}
-
地点： 辽宁8.00万
辽宁大学工商管理(MBA) 2.5年学制 周末班}
东北大学
沈阳师范大学
沈阳航空航天大学
沈阳工业大学
沈阳农业大学
微信小程序
微信公众号
在职研APP
